Heuristics and Undecidable Problems Teach Teach

Popcorn Hack #1

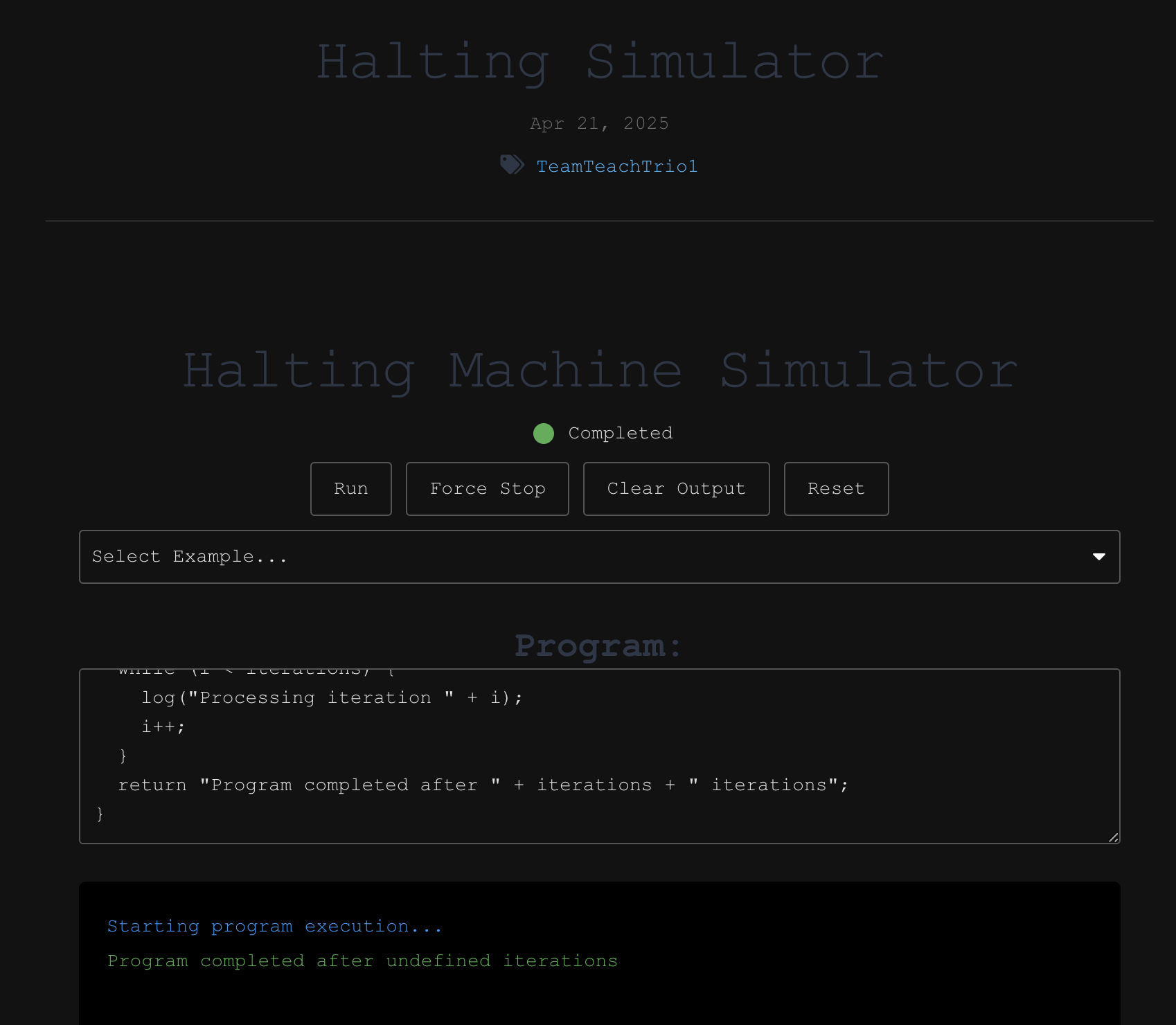
The Halting Machine Simulator lets you test whether a given program finishes running (halts) or loops forever, demonstrating the concept behind the Halting Problem. Proves that there’s no general algorithm that can determine whether every possible program/input combination halts or not. More generally, the halting problem is the problem of determining, from a description of an arbitrary computer program and an input, whether the program will finish running.

DFS (Depth First Search) - Popcorn Hack #2

graph = {
    'A': ['B', 'C', 'E'],
    'B': ['A', 'D'],
    'C': ['A', 'E'],
    'D': ['B', 'E'],
    'E': ['A', 'C', 'D']
}

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    
    visited.add(start)
    print(start, end=" ")
    
    for neighbor in graph[start]:
        if neighbor not in visited:
            dfs(graph, neighbor, visited)

# Using our example graph
dfs(graph, 'A')  # Output: A B D E C

A B D E C

BFS (Breadth First Search) Popcorn Hack #3

from collections import deque

def bfs(graph, start):
    visited = set()
    queue = deque([start])
    visited.add(start)
    
    while queue:
        vertex = queue.popleft()
        print(vertex, end=" ")
        
        for neighbor in graph[vertex]:
            if neighbor not in visited:
                visited.add(neighbor)
                queue.append(neighbor)

# Using our example graph
bfs(graph, 'A')  # Output: A B C E D

A B C E D

Practice Problems

MCQ 1

B: Algorithm II uses a heuristic approach to provide an approximate solution in reasonable time. Explanation: Algorithm II is implementing the Nearest Neighbor heuristic. While it may not find the optimal solution, it runs in polynomial time (O(n²)), which is considered reasonable, unlike Algorithm I which would take factorial time (O(n!)).

MCQ 2

D: There exist some problems that cannot be solved using any algorithm. Explanation: These are known as undecidable problems in computer science. No matter how powerful a computer is, or how advanced algorithms become, there are some problems (like the Halting Problem) that no algorithm can ever solve for all possible inputs.

Homework

Part 1:

Another real-life undecidable problem is checking if two computer programs always do the exact same thing (called program equivalence). Even if two programs look different, there’s no guaranteed way to tell if they’ll always give the same results for every possible input—no matter how smart your tools are—because this would also solve the Halting Problem.

Part 2

import math

def distance(a, b):
    return math.sqrt((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2)

def nearest_neighbor_tsp(cities):
    n = len(cities)
    visited = [False] * n
    path = []
    total_distance = 0.0

    current_city = 0
    path.append(current_city)
    visited[current_city] = True

    for _ in range(n - 1):
        nearest_city = None
        min_dist = float('inf')

        for i in range(n):
            if not visited[i]:
                dist = distance(cities[current_city], cities[i])
                if dist < min_dist:
                    min_dist = dist
                    nearest_city = i

        path.append(nearest_city)
        visited[nearest_city] = True
        total_distance += min_dist
        current_city = nearest_city

    # Return to starting city
    total_distance += distance(cities[current_city], cities[path[0]])
    path.append(path[0])  # Complete the cycle

    return path, total_distance

# Example usage
cities = [(0, 0), (2, 3), (5, 2), (6, 6), (8, 3)]
path, total_distance = nearest_neighbor_tsp(cities)
print("Visit order:", path)
print("Total distance:", total_distance)

Visit order: [0, 1, 2, 4, 3, 0]
Total distance: 22.020939245503307

Part 3

A real-world example of using heuristics is Google Maps when it finds the fastest driving route. The app uses quick guesses based on traffic, road types, and speed limits to find a good path. It doesn’t check every possible route because there are too many combinations, which would take too long. Instead, it picks a route that’s probably the fastest, even if it’s not perfect. This helps people get directions quickly without waiting for a computer to try every option.

Heuristics and Undecidable Problems Teach Teach